понедельник, 20 июля 2015 г.
Ответы на вопросы о проведении ЗНО по математике
Для обсуждения вопросов, касающихся следующих ЗНО по математике, подготовки к тестированию и обсуждению методов решения задач, открыт новый математический блог. Приглашаются все желающие!
среда, 16 мая 2012 г.
Решения пробного ЗНО 2012 по математике (задачи 29 - 32)
Задание 29. Планиметрия
На рисунке изображена траектория движения автомобиля из пункта А в пункт В. Она состоит из трёх прямолинейных участков: АК, КМ и МВ. Определите расстояние d между пунктами А и В, если АК = 60 км, КМ = 120 км, МВ = 100 км (все отрезки лежат в одной плоскости)
Решение
Если отрезок МВ параллельно перенести вправо так, чтобы точка М совпала с точкой В, а отрезок МВ перенести параллельно вниз так, чтобы его точка М совпала с точкой К, то расстояние d окажется гипотенузой прямоугольного треугольника с катетами 120 км и 60 + 100 = 160 (км). А это получается египетский треугольник, растянутый в 40 раз. Значит гипотенуза будет равна 5х40 = 200 (км)
Ответ: 200
Задание 30. Проценты. Текстовые задачи.
В один день гражданин заключил с двумя банками кредитные соглашения сроком на год. С первым банком – под 12% годовых, со вторым – под 15% годовых. Всего он получил в кредит 5000 гривен. Погашение кредитов происходит единоразовым платежом в последний день действия соглашения. Начисленная сумма процентов за пользование кредитами составляет 654 гривны. Сколько денег гражданин взял в кредит под бОльшие проценты?
Решение
Обозначим то, что нам надо узнать, а именно, сумму денег, взятую во втором банке, за х. Тогда в первом банке он взял 5000 – x гривен. В первом банке ему начислили 12% за год пользования кредитом, так что туда он переплатил 0,12(5000 – x) гривен. А во втором, где брал под 15%, переплата составила 0,15x (грн). А по условию всего было переплачено 654 грн. Имеем уравнение:
0,12(5000 – x) + 0,15x = 654
600 + 0,03x = 654
0,03x = 54
x = 1800
Значит, под бОльшие проценты он взлял 1800 гривен.
Ответ: 1800
Задание 31. Стереометрия. Призма.
Вокруг правильной треугольной призмы описана сфера радиуса 6 см. Радиус сферы, проведённый к вершине призмы, образует с боковым ребром угол в 30o. Найдите объём призмы (в см3)
Решение
Рассмотрим призму ABCA1B1C1
Опустим из центра описанной сферы О перпендикуляры ОN на боковое ребро и OO1 на основание. Точка N будет серединой бокового ребра, а точка O1 – центром описанной окружности. По условию угол OBN равен 30o. Тогда угол OBO1 составит 60o
Из треугольника OBN найдём
см, значит высота призмы 
см.
Из треугольника OBO1 найдём O1B = 3 см. Поскольку в равностороннем треугольнике со стороной а радиус описанной окружности равен
, то сторона основания 
. 
.
В таком случае площадь основания составит:
Объём же пирамиды – это произведение площади основания на высоту.
(см3)
Ответ: 121,5 см3
Задание 32. Логарифм. Уравнения с параметром.
Найдите все значения параметра а, при которых произведение корней уравнения log22x – (2a2 – a)log2x + 1 – 2a = 0 равняется восьми. Если такое а единственно, запишите его в ответ. Если таких значений больше одного, то в ответ запишите наименьшее из них.
Решение
ОДЗ: x > 0
Сделаем замену log2x = t. Тогда уравнение примет вид:
t2 – (2a2 – a)t + 1 – 2a = 0
если в исходном уравнении были корни x1 и x2 и x1x2 = 8, то каким должно быть соотношение между корнями t1 = log2x1 и t2 = log2x2 нового уравнения?
Прологарифмируем исходное соотношение
x1x2 = 8
log2(x1x2) = log28
log2x1 + log2x2 = 3
t1 + t2 = 3
Значит, сумма корней нового уравнения должна равняться трём. Но при этом они должны существовать, так что дискриминант его должен быть неотрицательным.
D = (2a2 – a)2 – 4(1 – 2a) = 4a4 – 4a3 + a2 + 8a – 4
В эту формулу будем потом подставлять найденные а.
Сумма корней квадратного уравнения – это коэффициент при первой степени неизвестного, взятый с противоположным знаком.
(2a2 – a) = 3
2a2 – a – 3 = 0
Корни:
a1 = -1. D = 4 + 4 + 1 – 8 – 4 < 0 Так что при этом значении параметра а действительных корней не будет вовсе.
a2 = 1,5. D = 20,25 – 13,5 + 2,25 + 12 – 4 > 0. А этот подходит.
Ответ: 1,5
На рисунке изображена траектория движения автомобиля из пункта А в пункт В. Она состоит из трёх прямолинейных участков: АК, КМ и МВ. Определите расстояние d между пунктами А и В, если АК = 60 км, КМ = 120 км, МВ = 100 км (все отрезки лежат в одной плоскости)Решение
Если отрезок МВ параллельно перенести вправо так, чтобы точка М совпала с точкой В, а отрезок МВ перенести параллельно вниз так, чтобы его точка М совпала с точкой К, то расстояние d окажется гипотенузой прямоугольного треугольника с катетами 120 км и 60 + 100 = 160 (км). А это получается египетский треугольник, растянутый в 40 раз. Значит гипотенуза будет равна 5х40 = 200 (км)
Ответ: 200
Задание 30. Проценты. Текстовые задачи.
В один день гражданин заключил с двумя банками кредитные соглашения сроком на год. С первым банком – под 12% годовых, со вторым – под 15% годовых. Всего он получил в кредит 5000 гривен. Погашение кредитов происходит единоразовым платежом в последний день действия соглашения. Начисленная сумма процентов за пользование кредитами составляет 654 гривны. Сколько денег гражданин взял в кредит под бОльшие проценты?
Решение
Обозначим то, что нам надо узнать, а именно, сумму денег, взятую во втором банке, за х. Тогда в первом банке он взял 5000 – x гривен. В первом банке ему начислили 12% за год пользования кредитом, так что туда он переплатил 0,12(5000 – x) гривен. А во втором, где брал под 15%, переплата составила 0,15x (грн). А по условию всего было переплачено 654 грн. Имеем уравнение:
0,12(5000 – x) + 0,15x = 654
600 + 0,03x = 654
0,03x = 54
x = 1800
Значит, под бОльшие проценты он взлял 1800 гривен.
Ответ: 1800
Задание 31. Стереометрия. Призма.
Вокруг правильной треугольной призмы описана сфера радиуса 6 см. Радиус сферы, проведённый к вершине призмы, образует с боковым ребром угол в 30o. Найдите объём призмы (в см3)
Решение
Рассмотрим призму ABCA1B1C1
Опустим из центра описанной сферы О перпендикуляры ОN на боковое ребро и OO1 на основание. Точка N будет серединой бокового ребра, а точка O1 – центром описанной окружности. По условию угол OBN равен 30o. Тогда угол OBO1 составит 60o
Из треугольника OBN найдём
Из треугольника OBO1 найдём O1B = 3 см. Поскольку в равностороннем треугольнике со стороной а радиус описанной окружности равен
В таком случае площадь основания составит:
Объём же пирамиды – это произведение площади основания на высоту.
Ответ: 121,5 см3
Задание 32. Логарифм. Уравнения с параметром.
Найдите все значения параметра а, при которых произведение корней уравнения log22x – (2a2 – a)log2x + 1 – 2a = 0 равняется восьми. Если такое а единственно, запишите его в ответ. Если таких значений больше одного, то в ответ запишите наименьшее из них.
Решение
ОДЗ: x > 0
Сделаем замену log2x = t. Тогда уравнение примет вид:
t2 – (2a2 – a)t + 1 – 2a = 0
если в исходном уравнении были корни x1 и x2 и x1x2 = 8, то каким должно быть соотношение между корнями t1 = log2x1 и t2 = log2x2 нового уравнения?
Прологарифмируем исходное соотношение
x1x2 = 8
log2(x1x2) = log28
log2x1 + log2x2 = 3
t1 + t2 = 3
Значит, сумма корней нового уравнения должна равняться трём. Но при этом они должны существовать, так что дискриминант его должен быть неотрицательным.
D = (2a2 – a)2 – 4(1 – 2a) = 4a4 – 4a3 + a2 + 8a – 4
В эту формулу будем потом подставлять найденные а.
Сумма корней квадратного уравнения – это коэффициент при первой степени неизвестного, взятый с противоположным знаком.
(2a2 – a) = 3
2a2 – a – 3 = 0
Корни:
a1 = -1. D = 4 + 4 + 1 – 8 – 4 < 0 Так что при этом значении параметра а действительных корней не будет вовсе.
a2 = 1,5. D = 20,25 – 13,5 + 2,25 + 12 – 4 > 0. А этот подходит.
Ответ: 1,5
Решения пробного ЗНО 2012 по математике (задачи 25 - 28)
Задание 25. Многочлены
Упростите выражение 2(a2 - 5ab + 4b2) - 3(2a2 - 2ab + 3b2) и вычислите его значение, если a = 1,1, b = 0,8
Решение
2(a2 - 5ab + 4b2) - 3(2a2 - 2ab + 3b2) = 2a2 - 10ab + 8b2 - 6a2 + 6ab - 9b2 = -4a2 - 4ab - b2 = -(2a + b) 2 = -(2,2 + 0,8) 2 = -9
Ответ: -9
Задание 26. Иррациональные уравнения
Решите уравнение
.
Если у уравнения 1 корень, запишите его в ответ. Если корней больше – укажите произведение всех корней. Если у уравнения нет корней, запишите в ответ число 100.
Решение
Находим ОДЗ: x > 2 и x > -0,5. Сильнейшее из этих неравенств x > 2.
Теперь можно возвести обе части в квадрат:
(x - 2)(2x + 1) = 3
2x2 – 3x – 2 = 3
2x2 – 3x – 5 = 0
Хотя уравнение и неприведённое, его тоже можно решить, задействовав теорему Виета. Получаем x1 = -1, не входит в ОДЗ, а x2 = 2,5 – подходит.
Ответ: 2,5
Задание 27. Наибольшее значение функции.
Найдите наибольшее значение функции y = 12x - x3 на отрезке [0; 3].
Решение
Функция – многочлен, разрывов не имеет, поэтому сначала возьмём производную.
y’ = 12 - 3x2
Приравняем её к нулю:
12 - 3x2 = 0
3x2 = 12
x2 = 4
x1 = -2
x2 = 2
Промежутку принадлежит только x2. Поэтому нам надо проверить значение функции в трёх точках: в ней и на краях промежутка.
y(0) = 0
y(2) = 24 – 8 = 16
y(3) = 36 – 27 = 9.
Наибольшим значением будет 16. Кстати, края можно было и не проверять, если, взяв вторую производную, убедиться, что в точке x = 2 именно максимум.
Ответ: 16
Задание 28. Комбинаторика
Сколько всего существует разных двузначных чисел, у которых первая цифра чётная, а вторая – нечётная?
Решение
Первой цифрой может быть: 2, 4, 6 или 8. Всего 4 варианта. Второй цифрой может быть: 1, 3, 5, 7, 9 – итого 5 вариантов. Значит, их комбинаций будет 4х5 = 20.
Ответ: 20
Упростите выражение 2(a2 - 5ab + 4b2) - 3(2a2 - 2ab + 3b2) и вычислите его значение, если a = 1,1, b = 0,8
Решение
2(a2 - 5ab + 4b2) - 3(2a2 - 2ab + 3b2) = 2a2 - 10ab + 8b2 - 6a2 + 6ab - 9b2 = -4a2 - 4ab - b2 = -(2a + b) 2 = -(2,2 + 0,8) 2 = -9
Ответ: -9
Задание 26. Иррациональные уравнения
Решите уравнение
Если у уравнения 1 корень, запишите его в ответ. Если корней больше – укажите произведение всех корней. Если у уравнения нет корней, запишите в ответ число 100.
Решение
Находим ОДЗ: x > 2 и x > -0,5. Сильнейшее из этих неравенств x > 2.
Теперь можно возвести обе части в квадрат:
(x - 2)(2x + 1) = 3
2x2 – 3x – 2 = 3
2x2 – 3x – 5 = 0
Хотя уравнение и неприведённое, его тоже можно решить, задействовав теорему Виета. Получаем x1 = -1, не входит в ОДЗ, а x2 = 2,5 – подходит.
Ответ: 2,5
Задание 27. Наибольшее значение функции.
Найдите наибольшее значение функции y = 12x - x3 на отрезке [0; 3].
Решение
Функция – многочлен, разрывов не имеет, поэтому сначала возьмём производную.
y’ = 12 - 3x2
Приравняем её к нулю:
12 - 3x2 = 0
3x2 = 12
x2 = 4
x1 = -2
x2 = 2
Промежутку принадлежит только x2. Поэтому нам надо проверить значение функции в трёх точках: в ней и на краях промежутка.
y(0) = 0
y(2) = 24 – 8 = 16
y(3) = 36 – 27 = 9.
Наибольшим значением будет 16. Кстати, края можно было и не проверять, если, взяв вторую производную, убедиться, что в точке x = 2 именно максимум.
Ответ: 16
Задание 28. Комбинаторика
Сколько всего существует разных двузначных чисел, у которых первая цифра чётная, а вторая – нечётная?
Решение
Первой цифрой может быть: 2, 4, 6 или 8. Всего 4 варианта. Второй цифрой может быть: 1, 3, 5, 7, 9 – итого 5 вариантов. Значит, их комбинаций будет 4х5 = 20.
Ответ: 20
Решения пробного ЗНО 2012 по математике (задачи 21 - 24, взаимосвязи)
Задание 21. Тригонометрия
К каждому выражению (1 – 4) подберите тождественно ему равное (А – Д).
Выражения
1. 1–cos2x
2. 2sinxcosx
3. cos2x-sin2x
4. (1-sinx)(1+sinx)
Преобразованные выражения
A. cos2x
Б. cos2x
В. sin2x
Г. –cos2x
Д. sin2x
Решение:
Приведу ссылку на приёмы того, как запомнить тригонометрические формулы. Зная самые простые из них, легко получается ответ.
Ответ:
1Д, 2В, 3Б, 4А
Задание 22. Стереометрия. Параллелепипед. Параллельность. Сечения.
ABCDA1B1C1D1 – прямоугольный параллелепипед. Каждой закрашенной плоскости (1 – 4) поставьте в соответствие параллельную ей прямую (А – Д)
Плоскость
Прямая
А. BC
Б. A1D
В. A1B
Г. BD
Д. DD1
Решение:
Прямая параллельна плоскости, если она параллельна хотя бы одной прямой, лежащей в плоскости. Поскольку в параллелепипеде есть три четвёрки параллельных рёбер, а также диагонали противоположных граней параллельны, это поможет найти правильные ответы.
Ответ:
1А, 2В, 3Д, 4Г.
Задание 23. Неравенства
Решите неравенства (1 – 4). Каждому неравенству поставьте в соответстсвие множество всех его решений (А – Д)
Неравенства
1. 5x-2>1
2.
3. log2x < 1
4. x2<4
Решения
А.)
Б. (-2;2)
В. (0;2)
Г.)
Д.)
Решение:
Первое неравенство, показательное, решается так:
5x - 2>1
5x - 2>50
x – 2 > 0
x > 2
Вариант Д.
Из решения второго неравенства, рационального, во-первых, следует исключить точку x = -2. Далее преобразовываем:
Числитель всегда положителен, значит, знак дроби зависит от знака знаменателя.
x + 2<0
x <-2
Вариант Г.
Третье неравенство, логарифмическое, имеет ОДЗ x > 0. Преобразовываем:
log2x < 1
log2x < log22
Т.к. основание больше нуля, знак логарифма просто убираем
x < 2
А с учётом ОДЗ это даст не вариант А (ловушку), а вариант В.
Четвёрное неравенство, квадратичное, решается тоже просто. После извлечения корня из обеих частей получим
|x| < 2
А, по правилам действий с модулями, оно его решением будет одновременное выполнение условий x < 2 и x > -2. Так что, здесь вариант Б.
Ответ:
1Д, 2Г, 3В, 4Б.
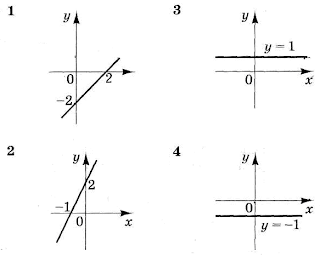
Задание 24. Графики функций
На каждом графике (1 – 4) изображена прямая. Каждой прямой поставьте в соответствие функцию (А – Д), график которой не имеет с этой прямой общих точек.
Графики
Функции
А. y = x
Б. y = log2x
В. y = (x-2)2
Г.
Д. y = x3
Решение:
Достаточно вспомнить, как выглядят графики функций. Кстати, для их построения можно воспользоваться отличным сервисом Вольфрам-Альфа.
Например, y = x и график 1 будут параллельны, и, следовательно, не иметь общих точек.
y = log2x не будет заходить в левую полуплоскость, а в правой будет расти медленнее, чем линейная функция. Поэтому он не пересечётся с графиком 2.
y = (x-2)2 находится только в верхней полуплоскости, поэтому он не будет иметь общих точек с прямой 4.
А прямая 3 будет асимптотой (кстати, знаете, как запомнить, почему там одна буква «с»?) для графика функции Г.
Ответ: 1А, 2Б, 3Г, 4В
К каждому выражению (1 – 4) подберите тождественно ему равное (А – Д).
Выражения
1. 1–cos2x
2. 2sinxcosx
3. cos2x-sin2x
4. (1-sinx)(1+sinx)
Преобразованные выражения
A. cos2x
Б. cos2x
В. sin2x
Г. –cos2x
Д. sin2x
Решение:
Приведу ссылку на приёмы того, как запомнить тригонометрические формулы. Зная самые простые из них, легко получается ответ.
Ответ:
1Д, 2В, 3Б, 4А
Задание 22. Стереометрия. Параллелепипед. Параллельность. Сечения.
ABCDA1B1C1D1 – прямоугольный параллелепипед. Каждой закрашенной плоскости (1 – 4) поставьте в соответствие параллельную ей прямую (А – Д)
Плоскость
А. BC
Б. A1D
В. A1B
Г. BD
Д. DD1
Решение:
Прямая параллельна плоскости, если она параллельна хотя бы одной прямой, лежащей в плоскости. Поскольку в параллелепипеде есть три четвёрки параллельных рёбер, а также диагонали противоположных граней параллельны, это поможет найти правильные ответы.
Ответ:
1А, 2В, 3Д, 4Г.
Задание 23. Неравенства
Решите неравенства (1 – 4). Каждому неравенству поставьте в соответстсвие множество всех его решений (А – Д)
Неравенства
1. 5x-2>1
2.
3. log2x < 1
4. x2<4
Решения
А.
Б. (-2;2)
В. (0;2)
Г.
Д.
Решение:
Первое неравенство, показательное, решается так:
5x - 2>1
5x - 2>50
x – 2 > 0
x > 2
Вариант Д.
Из решения второго неравенства, рационального, во-первых, следует исключить точку x = -2. Далее преобразовываем:
Числитель всегда положителен, значит, знак дроби зависит от знака знаменателя.
x + 2<0
x <-2
Вариант Г.
Третье неравенство, логарифмическое, имеет ОДЗ x > 0. Преобразовываем:
log2x < 1
log2x < log22
Т.к. основание больше нуля, знак логарифма просто убираем
x < 2
А с учётом ОДЗ это даст не вариант А (ловушку), а вариант В.
Четвёрное неравенство, квадратичное, решается тоже просто. После извлечения корня из обеих частей получим
|x| < 2
А, по правилам действий с модулями, оно его решением будет одновременное выполнение условий x < 2 и x > -2. Так что, здесь вариант Б.
Ответ:
1Д, 2Г, 3В, 4Б.
Задание 24. Графики функций
На каждом графике (1 – 4) изображена прямая. Каждой прямой поставьте в соответствие функцию (А – Д), график которой не имеет с этой прямой общих точек.
Графики
 |
А. y = x
Б. y = log2x
В. y = (x-2)2
Г.
Д. y = x3
Решение:
Достаточно вспомнить, как выглядят графики функций. Кстати, для их построения можно воспользоваться отличным сервисом Вольфрам-Альфа.
Например, y = x и график 1 будут параллельны, и, следовательно, не иметь общих точек.
y = log2x не будет заходить в левую полуплоскость, а в правой будет расти медленнее, чем линейная функция. Поэтому он не пересечётся с графиком 2.
y = (x-2)2 находится только в верхней полуплоскости, поэтому он не будет иметь общих точек с прямой 4.
А прямая 3 будет асимптотой (кстати, знаете, как запомнить, почему там одна буква «с»?) для графика функции Г.
Ответ: 1А, 2Б, 3Г, 4В
вторник, 15 мая 2012 г.
Решения пробного ЗНО 2012 по математике (задачи 16 - 20)
Задание 16. Стереометрия. Цилиндр.
Цилиндр, радиус основания которого равен 4 см, высота – 12 см, разрезали плоскостью, параллельной основанию. Получилось 2 цилиндра (см. рис.). Чему равна их суммарная площадь полной поверхности.
Варианты ответа:
А
см2; Б 
см2; В 
см2; Г 
см2; Д 
см2;
Решение:
Когда большой цилиндр разрезали, образовалось 2 дополнительных основания. Значит, искомая полная поверхность равна Sбок + 4 Sосн =
(см2)
Ответ: Д см2
Задание 17. Иррациональные числа
Упростите выражение
Варианты ответа:
А 2; Б
; В 
; Г 
; Д 
;
Решение:
Если в знаменателе дроби есть иррациональное выражение, её числитель и знаменатель нужно домножить на такое выражение, которое устранило иррациональность оттуда. В данном случае, нужно домножить на
. Получим:
(\sqrt{2}-1)}{(\sqrt{2}+%2B+1)(\sqrt{2}-1)} = \frac{4+%2B+\sqrt{2}-2\sqrt{2}-1}{2-1} = 3-\sqrt{2})
Ответ: Д
Задание 18. Текстовые задачи. Планиметрия. Длина окружности.
На рисунке изображён эскиз эмблемы фирмы N. Эмблема имеет форму окружности, внутри которой расположены 3 одинаковых полуокружности. Один конец каждой полуокружности совпадает с центром большой окружности, а другой лежит на ней. Нужно изготовить эмблему радиусом 2 м. Все её элементы будут сделаны из гибкого материала ценой 100 гривен за 1 метр длины. Укажите среди приведённых сумм наименьшую, которой хватит на приобретение материала для эмблемы. Считайте, что места соединения элементов эмблемы, обозначенные точками на рисунке, не требуют дополнительных затрат.
Варианты ответа:
А 3000 грн.; Б 2720 грн.; В 2540 грн.; Г 2310 грн.; Д 2170 грн.;
Решение:
Длина внешней окружности равна
(м). Каждая из внутренних полуокружностей имеет радиус 1 м, значит, их суммарная длина равна 
м. Итого 
м. Воспользовавшись приближением 
, получим, что заплатить потребуется примерно 2200 грн. Наименьшая из приведённых сумм, которой хватит на покупку, это 2310 грн. Она и будет ответом.
Ответ: Г 2310 грн.
Задание 19. Интеграл. Производная
Какая из приведённых функций является первообразной для функции f(x) = 2 + sin2x?
Варианты ответа:
А F(x) = 2x - 0,5cos2x; Б F(x) = 2x + 0,5cos2x; В F(x) = 2x + 2cos2x; Г F(x) = 2cos2x; Д F(x) = 2x - cos2x;
Решение:
Возьмём интеграл
При С = 0 это будет вариант А.
Ответ: А F(x) = 2x - 0,5cos2x;
Задание 20. Графики функций
На одном из рисунков изображён эскиз графика
. Укажите его.
Варианты ответа:
Решение:
Если перед аргументом функции стоит знак минус, то график отражается относительно оси ординат. Поэтому правильным ответом будет вариант Г.
Ответ: Г.
Цилиндр, радиус основания которого равен 4 см, высота – 12 см, разрезали плоскостью, параллельной основанию. Получилось 2 цилиндра (см. рис.). Чему равна их суммарная площадь полной поверхности.
Варианты ответа:
А
Решение:
Когда большой цилиндр разрезали, образовалось 2 дополнительных основания. Значит, искомая полная поверхность равна Sбок + 4 Sосн =
Ответ: Д
Задание 17. Иррациональные числа
Упростите выражение
Варианты ответа:
А 2; Б
Решение:
Если в знаменателе дроби есть иррациональное выражение, её числитель и знаменатель нужно домножить на такое выражение, которое устранило иррациональность оттуда. В данном случае, нужно домножить на
Ответ: Д
Задание 18. Текстовые задачи. Планиметрия. Длина окружности.
На рисунке изображён эскиз эмблемы фирмы N. Эмблема имеет форму окружности, внутри которой расположены 3 одинаковых полуокружности. Один конец каждой полуокружности совпадает с центром большой окружности, а другой лежит на ней. Нужно изготовить эмблему радиусом 2 м. Все её элементы будут сделаны из гибкого материала ценой 100 гривен за 1 метр длины. Укажите среди приведённых сумм наименьшую, которой хватит на приобретение материала для эмблемы. Считайте, что места соединения элементов эмблемы, обозначенные точками на рисунке, не требуют дополнительных затрат.Варианты ответа:
А 3000 грн.; Б 2720 грн.; В 2540 грн.; Г 2310 грн.; Д 2170 грн.;
Решение:
Длина внешней окружности равна
Ответ: Г 2310 грн.
Задание 19. Интеграл. Производная
Какая из приведённых функций является первообразной для функции f(x) = 2 + sin2x?
Варианты ответа:
А F(x) = 2x - 0,5cos2x; Б F(x) = 2x + 0,5cos2x; В F(x) = 2x + 2cos2x; Г F(x) = 2cos2x; Д F(x) = 2x - cos2x;
Решение:
Возьмём интеграл
При С = 0 это будет вариант А.
Ответ: А F(x) = 2x - 0,5cos2x;
Задание 20. Графики функций
На одном из рисунков изображён эскиз графика
Варианты ответа:
Решение:
Если перед аргументом функции стоит знак минус, то график отражается относительно оси ординат. Поэтому правильным ответом будет вариант Г.
Ответ: Г.
воскресенье, 13 мая 2012 г.
Решения пробного ЗНО 2012 по математике (задачи 11-15)
Задание 11. Системы уравнений
Сколько решений имеет система уравнений:
Варианты ответа:
А ни одного; Б один; В два; Г три; Д более трёх;
Решение:
Сложив уравнения системы, получим: 2x2 = -2. Это уравнение решений в действительных числах не имеет, значит, и у исходной системы корней нет.
Ответ: А ни одного
Задание 12. Арифметическая прогрессия.
Из аэропорта авиарейсы по расписанию производятся каждые 10 минут. Первый самолёт вылетел в 6 часов утра. В котором часу по расписанию будет вылет 30-го самолёта?
Варианты ответа:
А 10 ч 40 мин; Б 10 ч 50 мин; В 11 ч 00 мин; Г 11 ч 30 мин; Д 12 ч 00 мин;
Решение:
Вылет 30-го самолёта произойдёт через 29 10-тиминутных интервалов, т.е. через 290 минут. Этот составит 4 часа 50 минут. Выходит, вылет запланирован на 10 ч 50 мин.
Ответ: Б 10 ч 50 мин
Задание 13. Логарифм
Вычислите log216
Варианты ответа:
А
; Б 
; В 1; Г 8; Д 12;
Решение:
Преобразуем данный логарифм:
(Потому, что показатель степени из основания логарифма выходит как знаменатель, а из логарифмируемого выражения – как числитель дроби-коэффициента перед логарифмом)
Ответ: Б
Задание 14. Стереометрия. Пирамида. Объём
Сторона основания правильной четырёхугольной пирамиды равна 4 см, а объём – 64 см 3. Найдите высоту пирамиды.
текст
Варианты ответа:
А см; Б 4 см; В 8 см; Г 12 см; Д 16 см;
Решение:
Объём пирамиды втрое меньше произведения площади основания на высоту. Площадь основания равна 42 = 16 (см2). Значит, высота её равна
(см)
Ответ: Г 12 см
Задание 15. Уравнения. Модули.
У какого из приведённых уравнений бесчисленное множество корней?
Варианты ответа:
А
; Б x = –x; В |x| = x; Г |–x| = 2; Д |x| = –3;
Решение:
У первого уравнения корней нет совсем, т.к. косинус не может превосходить единицы. У второго единственный корень: x = 0. А вот третьему удовлетворяют все неотрицательные числа. Дальше перебирать не стоит – ответ найден.
Ответ: В |x| = x
Сколько решений имеет система уравнений:
Варианты ответа:
А ни одного; Б один; В два; Г три; Д более трёх;
Решение:
Сложив уравнения системы, получим: 2x2 = -2. Это уравнение решений в действительных числах не имеет, значит, и у исходной системы корней нет.
Ответ: А ни одного
Задание 12. Арифметическая прогрессия.
Из аэропорта авиарейсы по расписанию производятся каждые 10 минут. Первый самолёт вылетел в 6 часов утра. В котором часу по расписанию будет вылет 30-го самолёта?
Варианты ответа:
А 10 ч 40 мин; Б 10 ч 50 мин; В 11 ч 00 мин; Г 11 ч 30 мин; Д 12 ч 00 мин;
Решение:
Вылет 30-го самолёта произойдёт через 29 10-тиминутных интервалов, т.е. через 290 минут. Этот составит 4 часа 50 минут. Выходит, вылет запланирован на 10 ч 50 мин.
Ответ: Б 10 ч 50 мин
Задание 13. Логарифм
Вычислите log216
Варианты ответа:
А
Решение:
Преобразуем данный логарифм:
Ответ: Б
Задание 14. Стереометрия. Пирамида. Объём
Сторона основания правильной четырёхугольной пирамиды равна 4 см, а объём – 64 см 3. Найдите высоту пирамиды.
текст
Варианты ответа:
А
Решение:
Объём пирамиды втрое меньше произведения площади основания на высоту. Площадь основания равна 42 = 16 (см2). Значит, высота её равна
Ответ: Г 12 см
Задание 15. Уравнения. Модули.
У какого из приведённых уравнений бесчисленное множество корней?
Варианты ответа:
А
Решение:
У первого уравнения корней нет совсем, т.к. косинус не может превосходить единицы. У второго единственный корень: x = 0. А вот третьему удовлетворяют все неотрицательные числа. Дальше перебирать не стоит – ответ найден.
Ответ: В |x| = x
Подписаться на:
Сообщения (Atom)